Optimal Control and Avoidance Using HJR
The project focuses on optimizing the control of a Dubins vehicle, which follows a path with constrained curvature. The primary goal is to develop strategies for avoiding obstacles and reaching targets efficiently.
Dubins Dynamics
Dubins vehicles are characterized by their nonholonomic constraints, limiting their turning capabilities. This project utilizes the vehicle's dynamics to compute optimal paths to a target while avoiding obstacles.
Minimum Time Dubins
Four possible paths (LSR, LSL, RSR, RSL) are considered to find the minimum time route.
Minimum Time-Avoid Problem
A distance-based penalty function is introduced to ensure the vehicle avoids obstacles.
Hamilton Jacobi Reachability (HJR)
The approach involves solving a partial differential equation using dynamic programming. The cost function and value function are key components, helping to compute the optimal control strategies.
Results
6 Pillar Simulation
Simulation results with six obstacles.
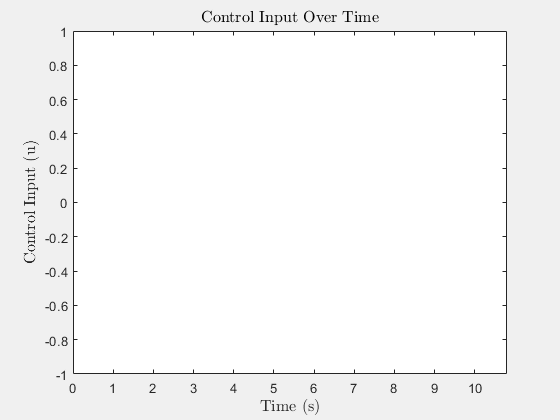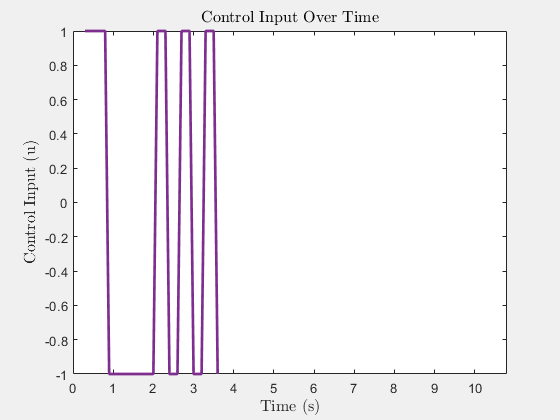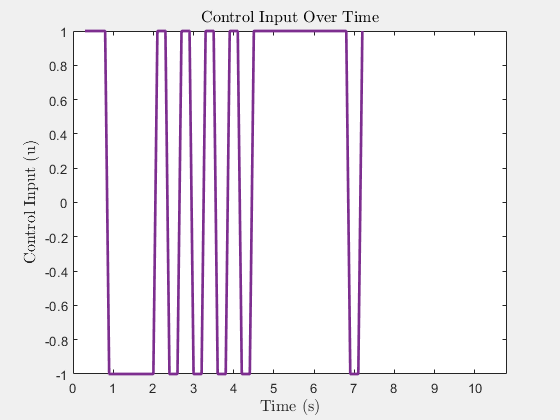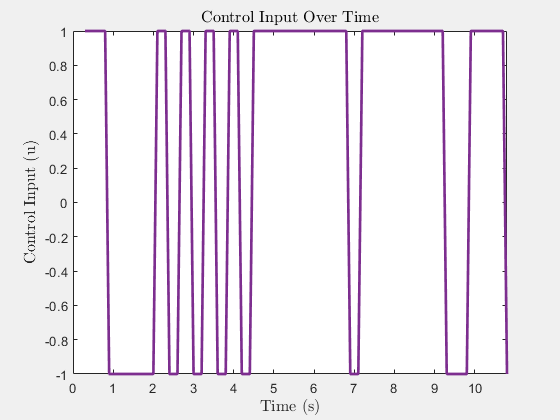
Control Input
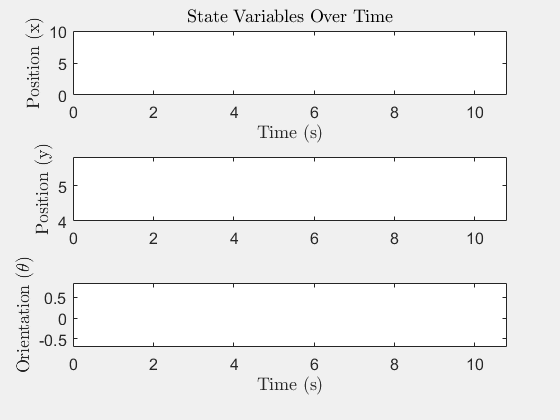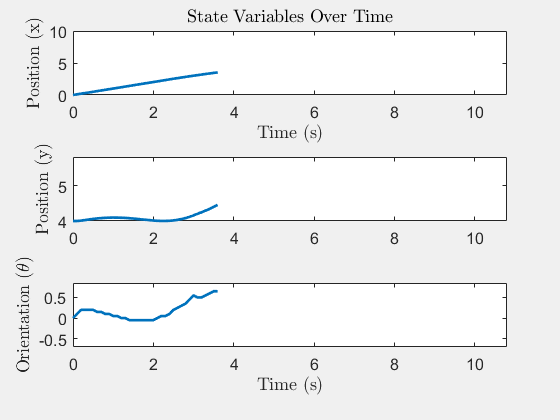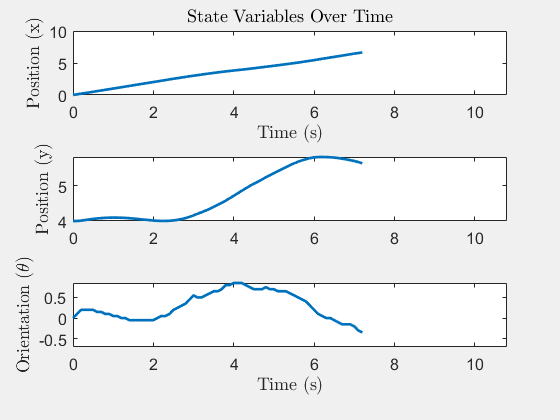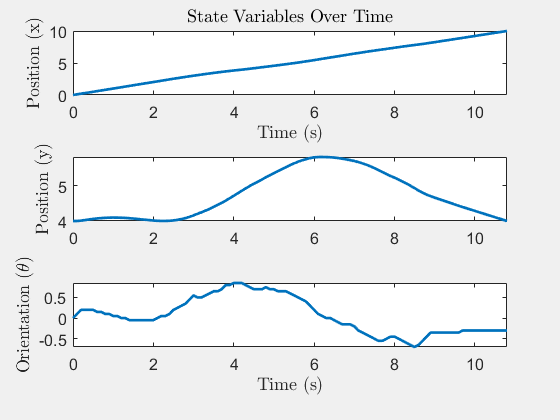
System States
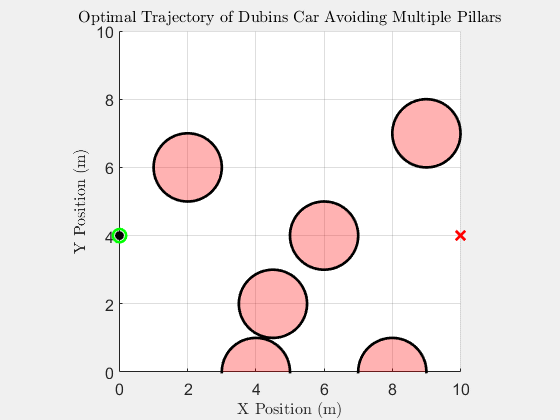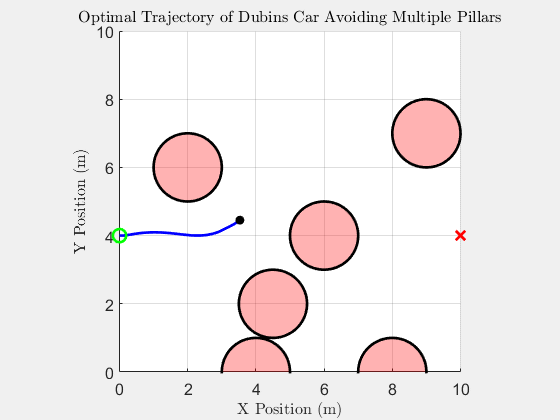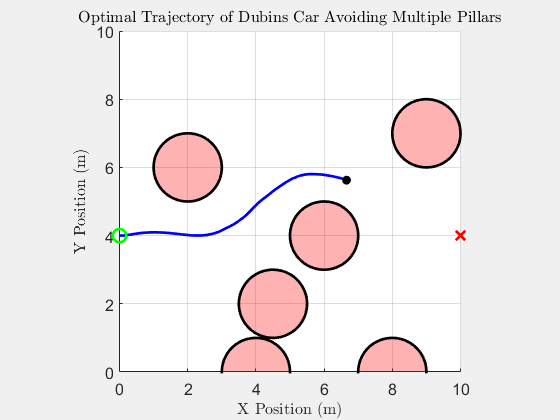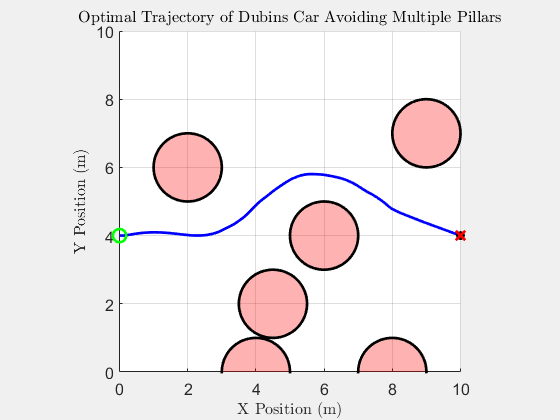
Top Down Trajectory
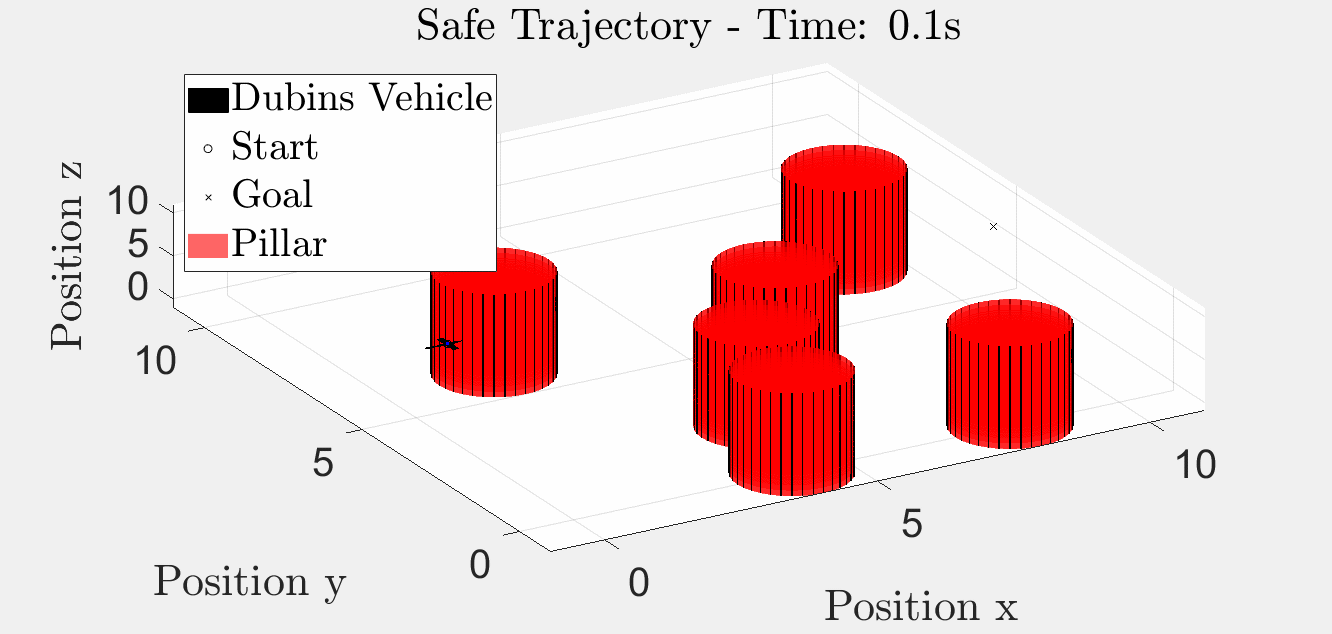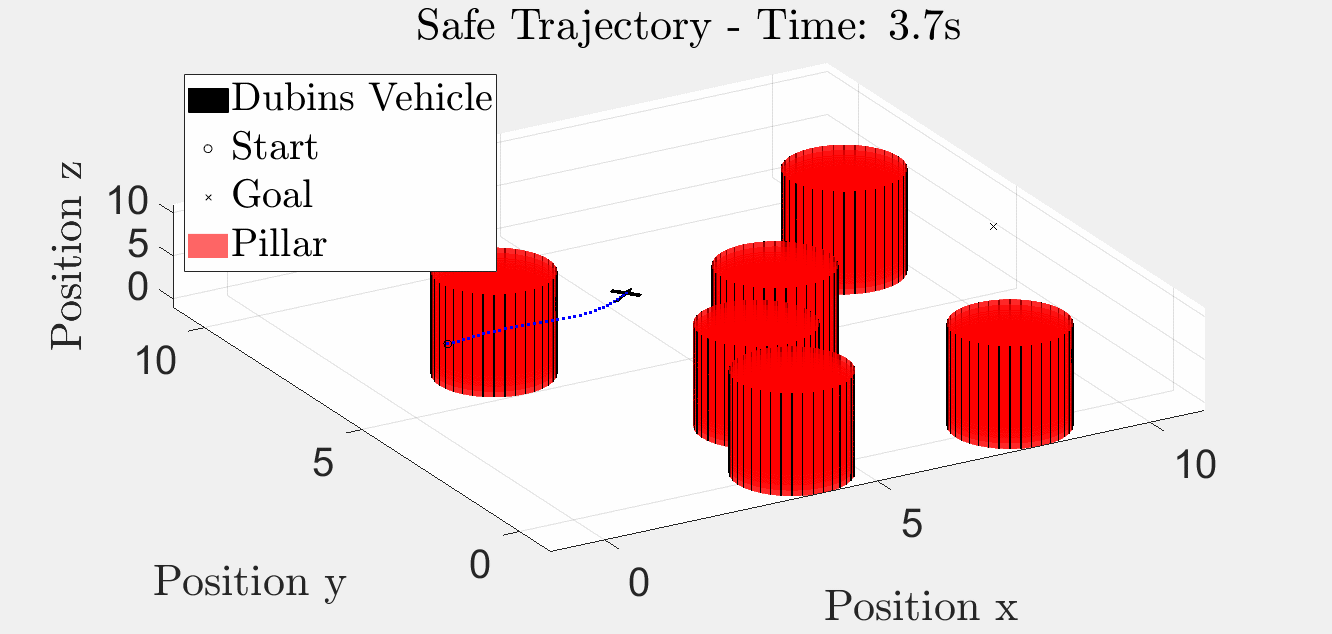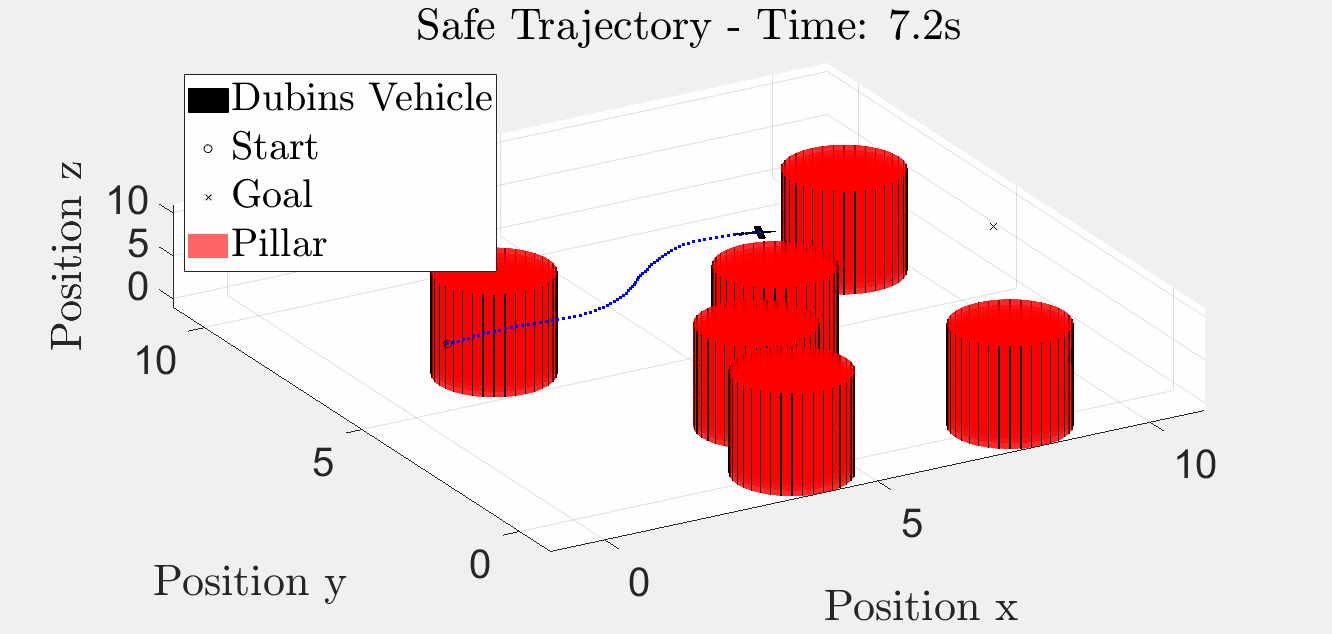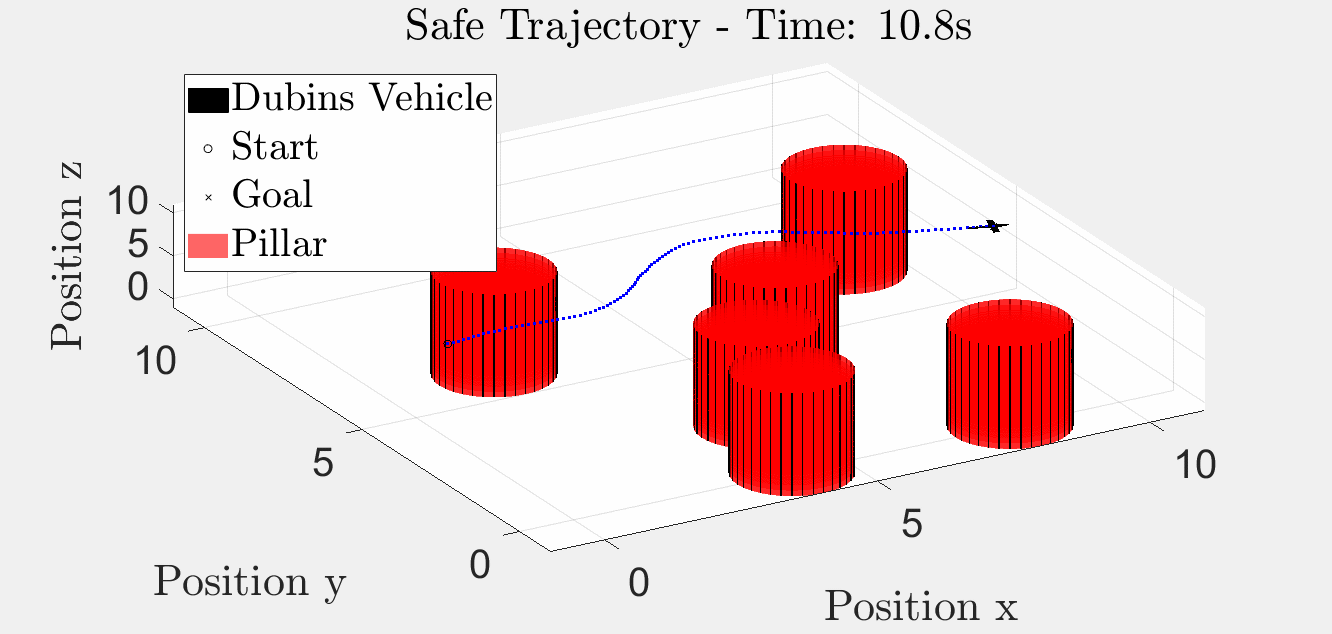
3D Trajectory
6 Pillar with YAPPS (MATLAB)
Simulation results with six obstacles using YAPPS.
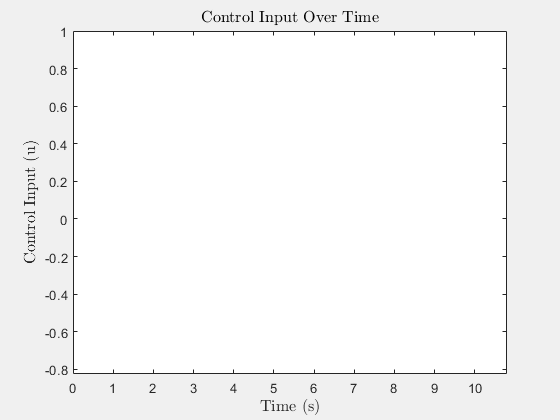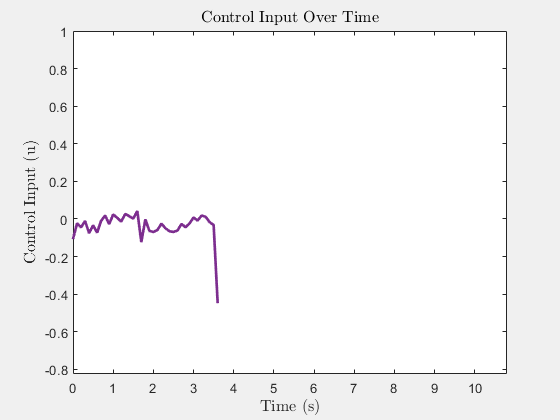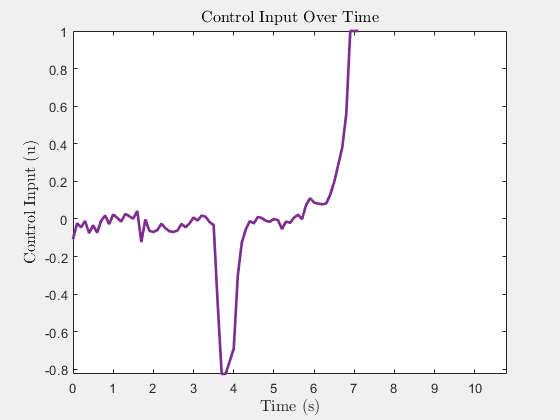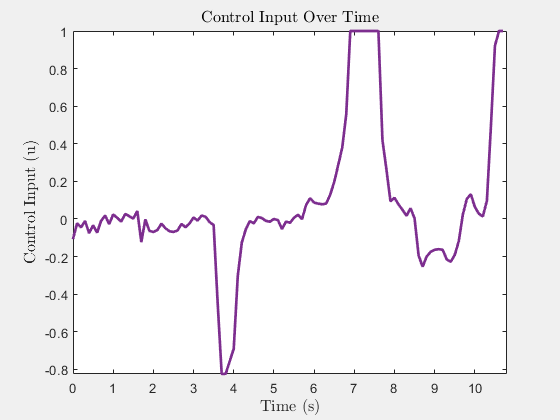
Control Input
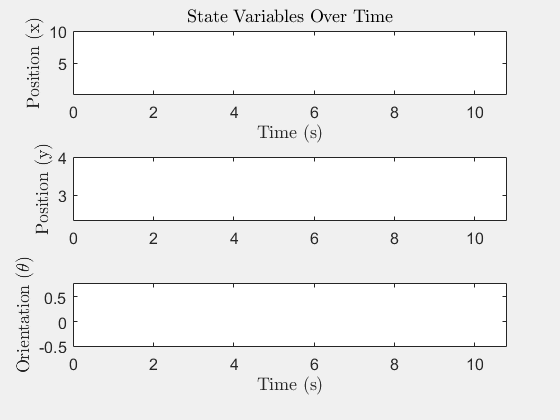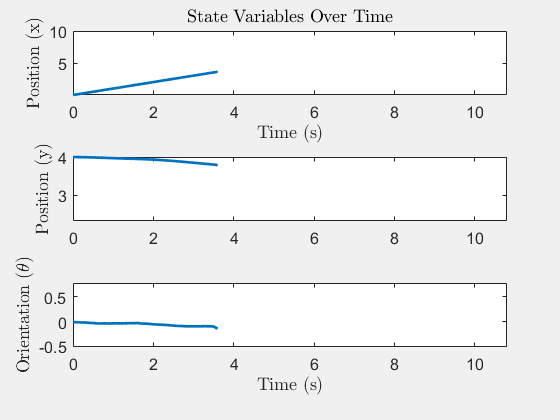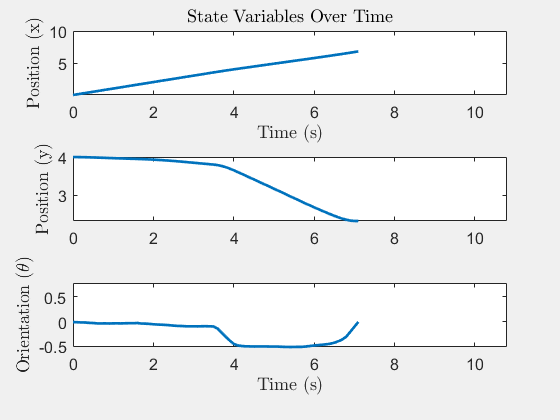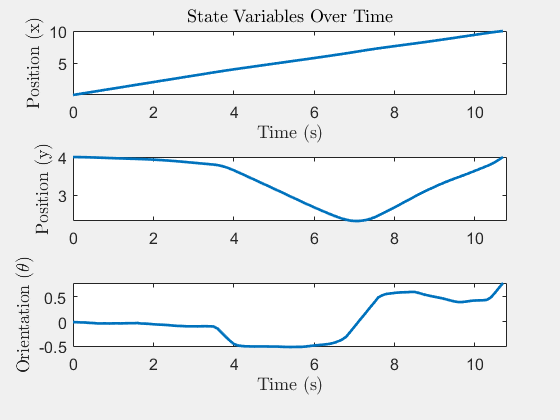
System States
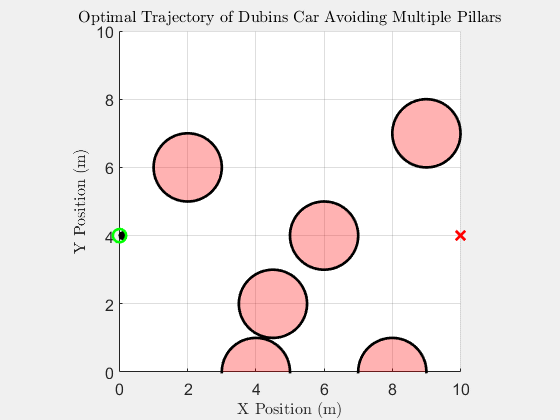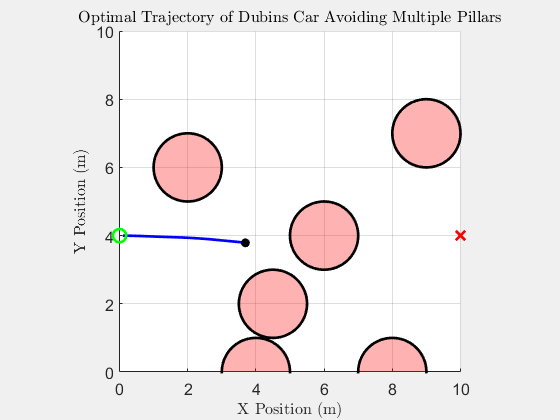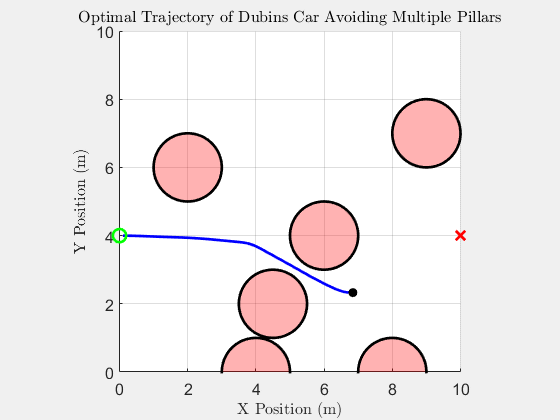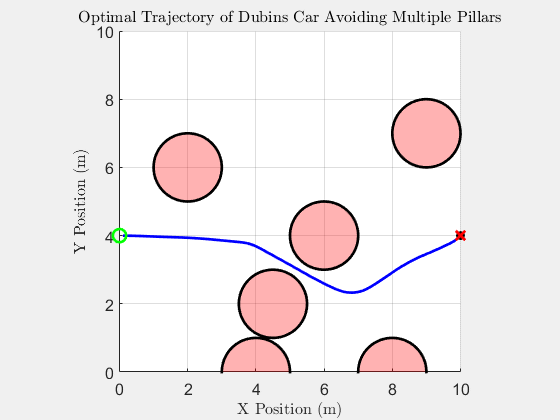
Top Down Trajectory
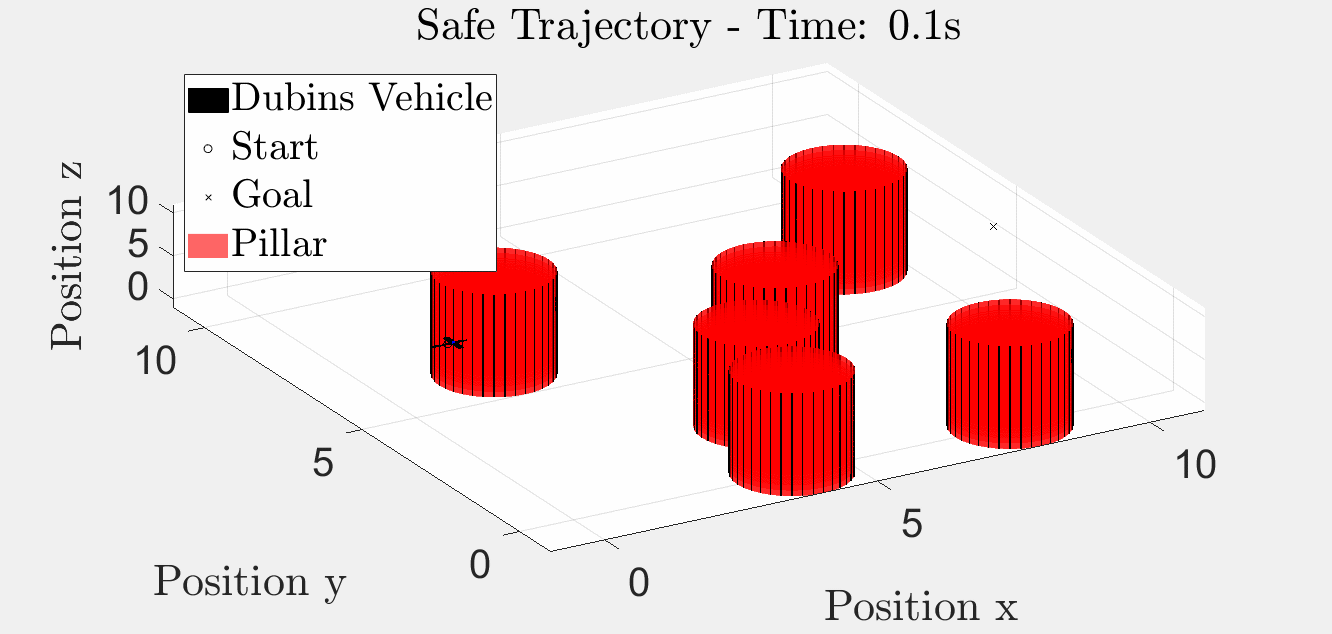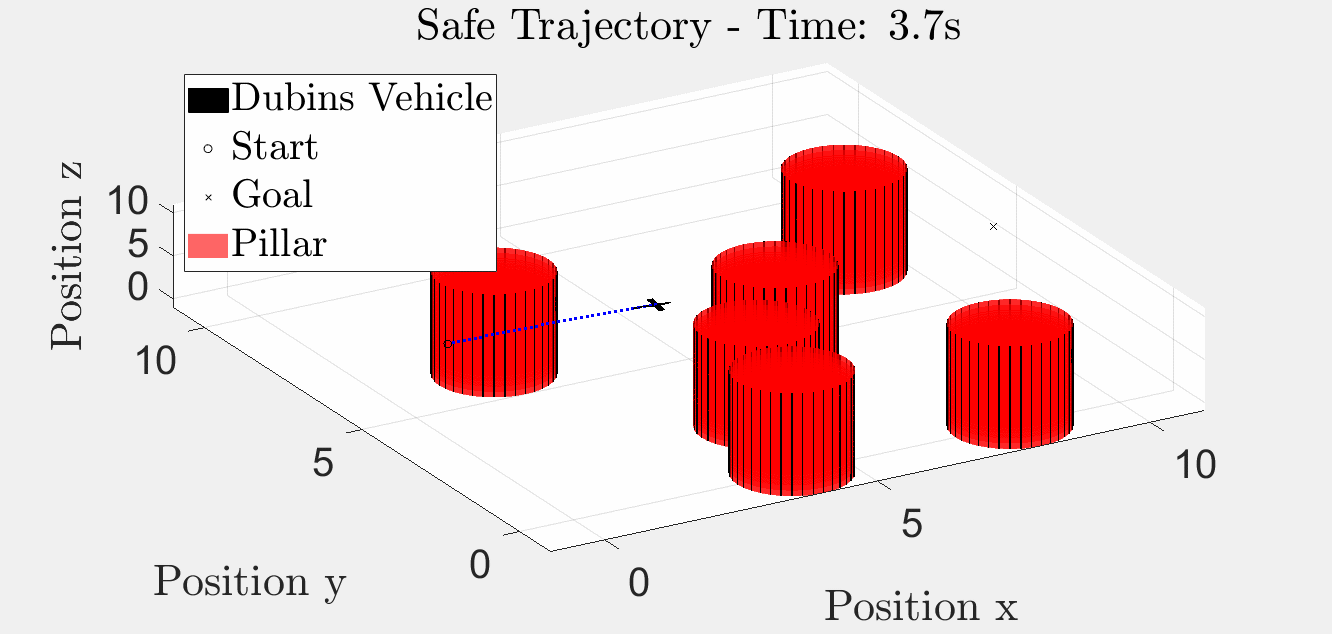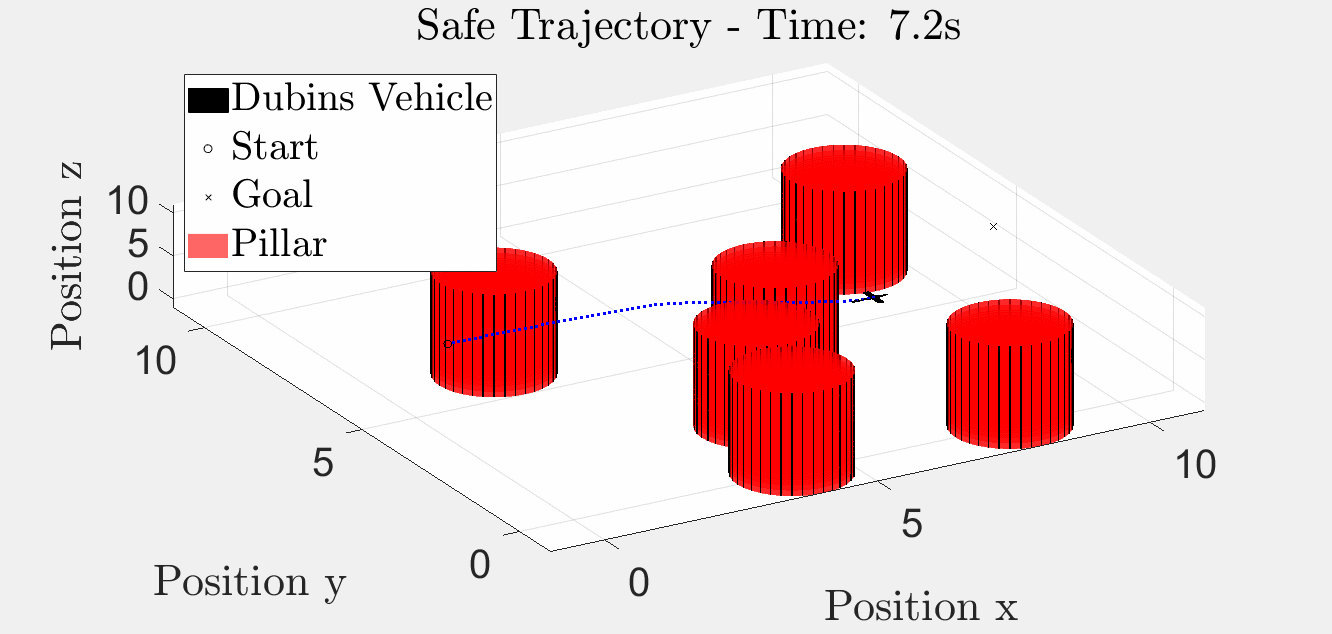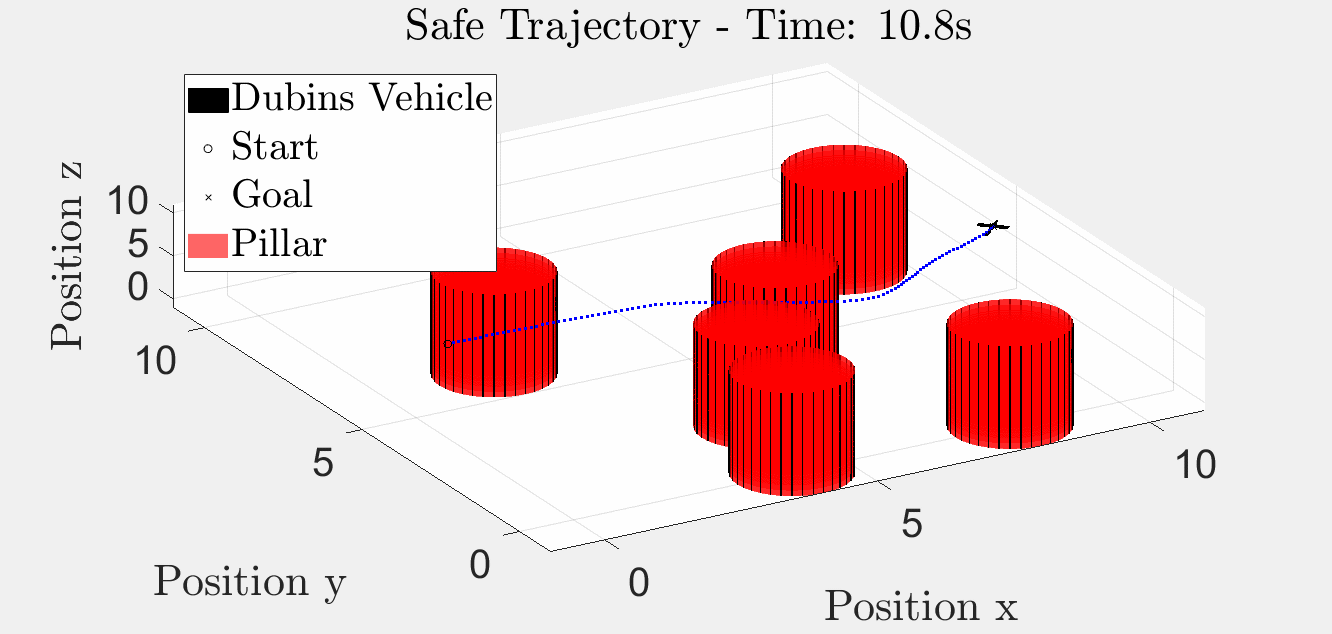
3D Trajectory
Conclusion and Future Work
The project highlights challenges such as grid discretization and computational time. Future work aims to extend the approach to 3D Dubins dynamics and explore control barrier functions.