Dubins Adaptive Control
Abstract
The control of a Dubins Vehicle when subjected to a loss of control effectiveness in the turning rate is considered. A complex state-space representation is used to model the vehicle dynamics. An adaptive control design is proposed, with the underlying stability analysis guaranteeing closed-loop boundedness and tracking of a desired path. It is shown that a path constructed by waypoints and a minimum turn radius can be specified using a reference model which can be followed by the closed loop system. The control design utilizes the complex representation as well as a PID controller for the nominal closed-loop. How the design can be modified to ensure path following even in the presence of input constraints is also discussed. Simulation studies are carried out to complement the theoretical derivations.
Simulation & Animations
In both examples below, an anomaly occurs between waypoints 1 and 2 which compromises the turning capabilities of the system.
Figure 1

Figure 1: Shows a Dubins Vehicle (DV) following a path constructed by waypoints. In red we have a PID controller and in blue we have an adaptive controller (AC). The AC ensures that the vehicle can follow the path even when subjected to a loss of control effectiveness. In both examples, an anomaly occurs between waypoints 1 and 2, compromising the turning capabilities of the system. The adaptive controller design ensures that the vehicle can follow the path even under such circumstances by learning the LOE online and adapting in real time.
Figure 2
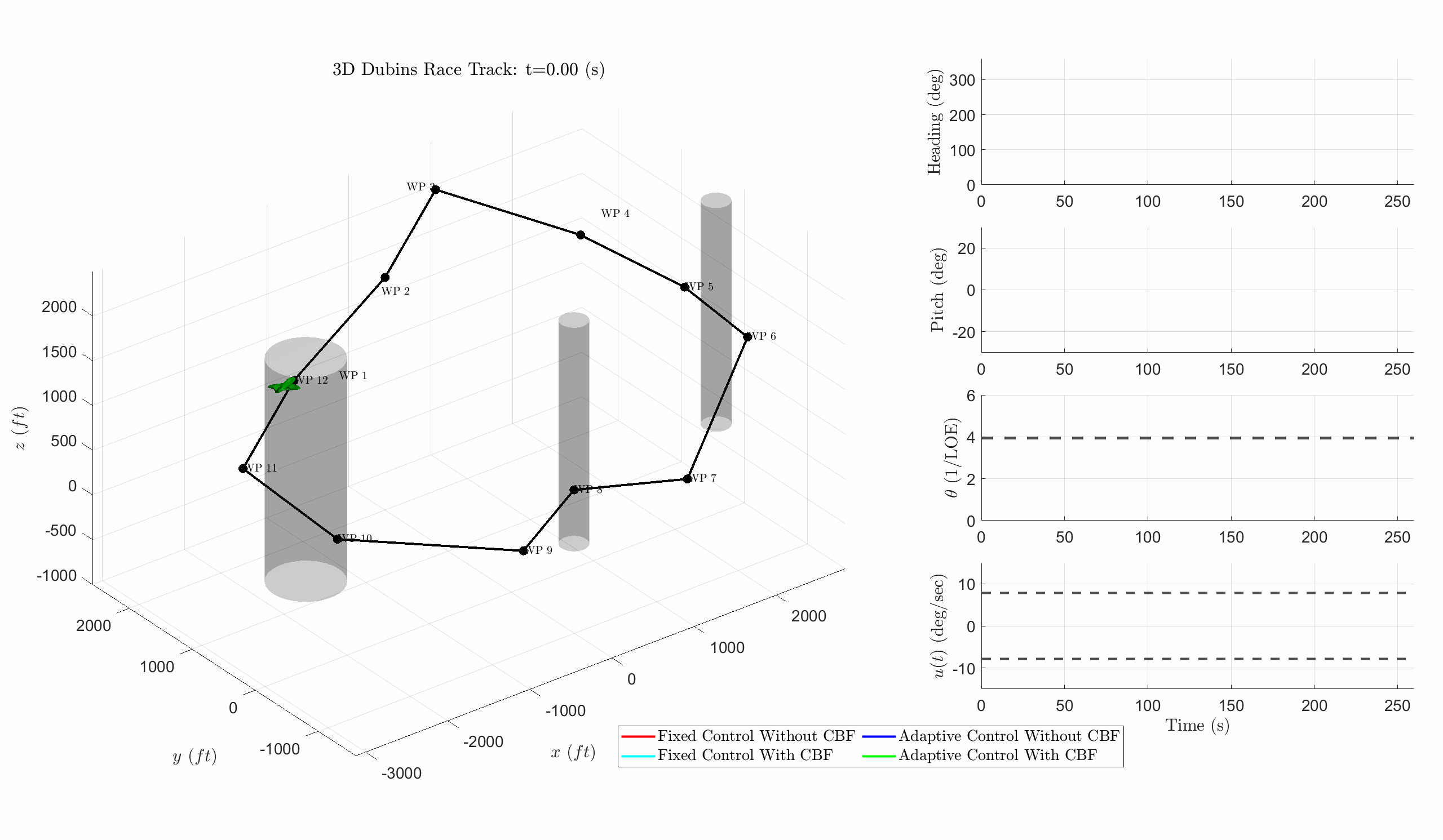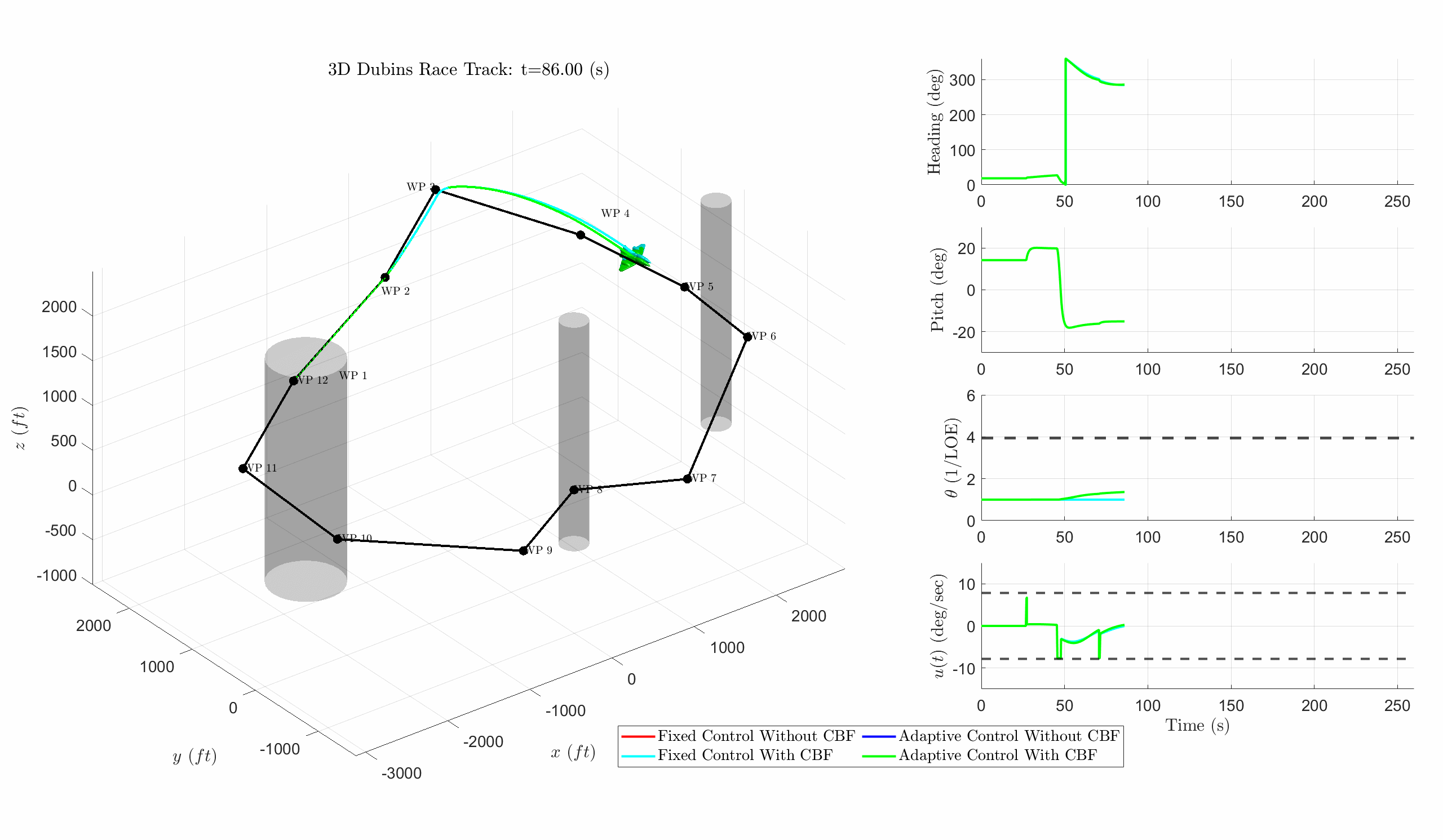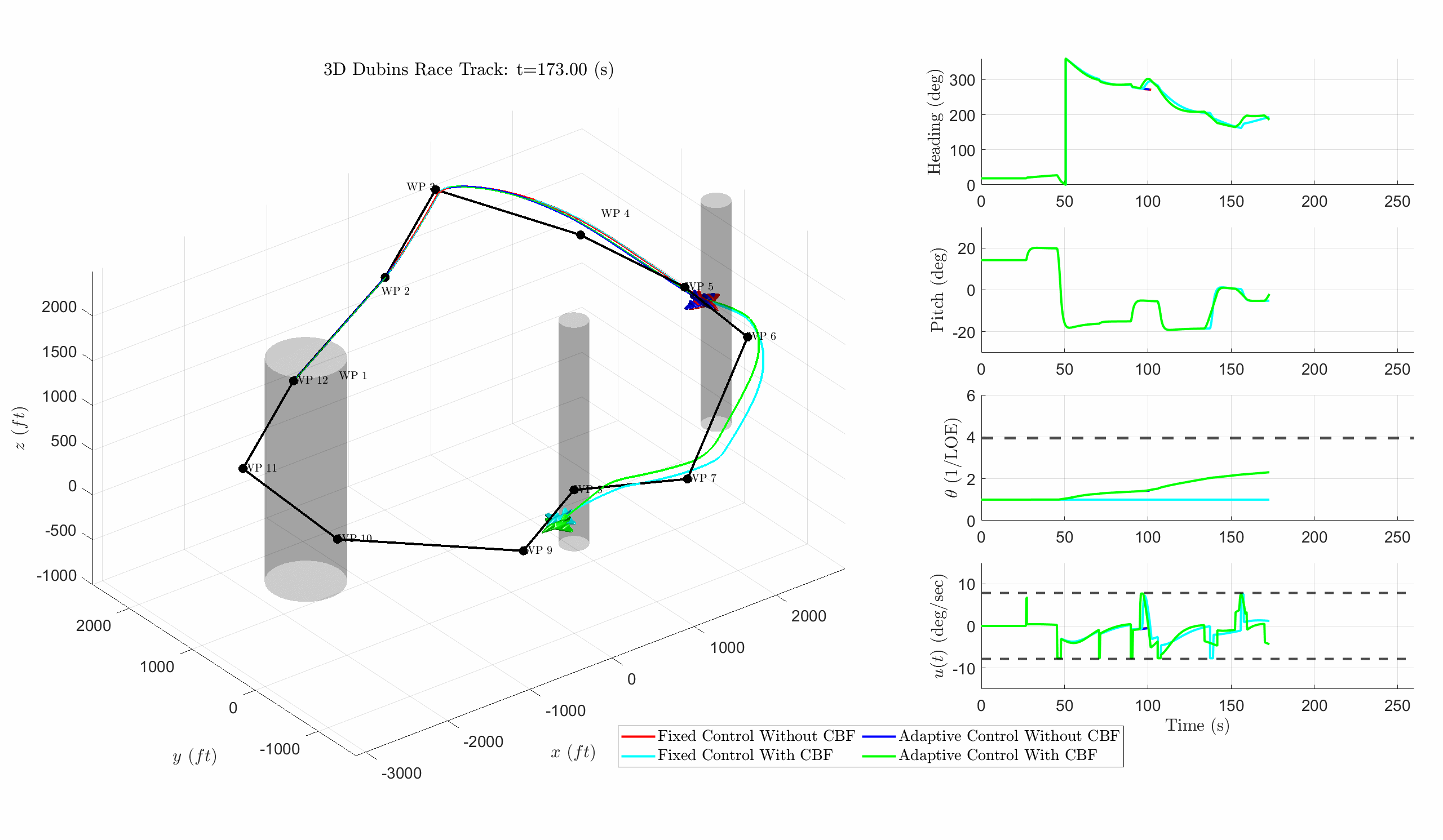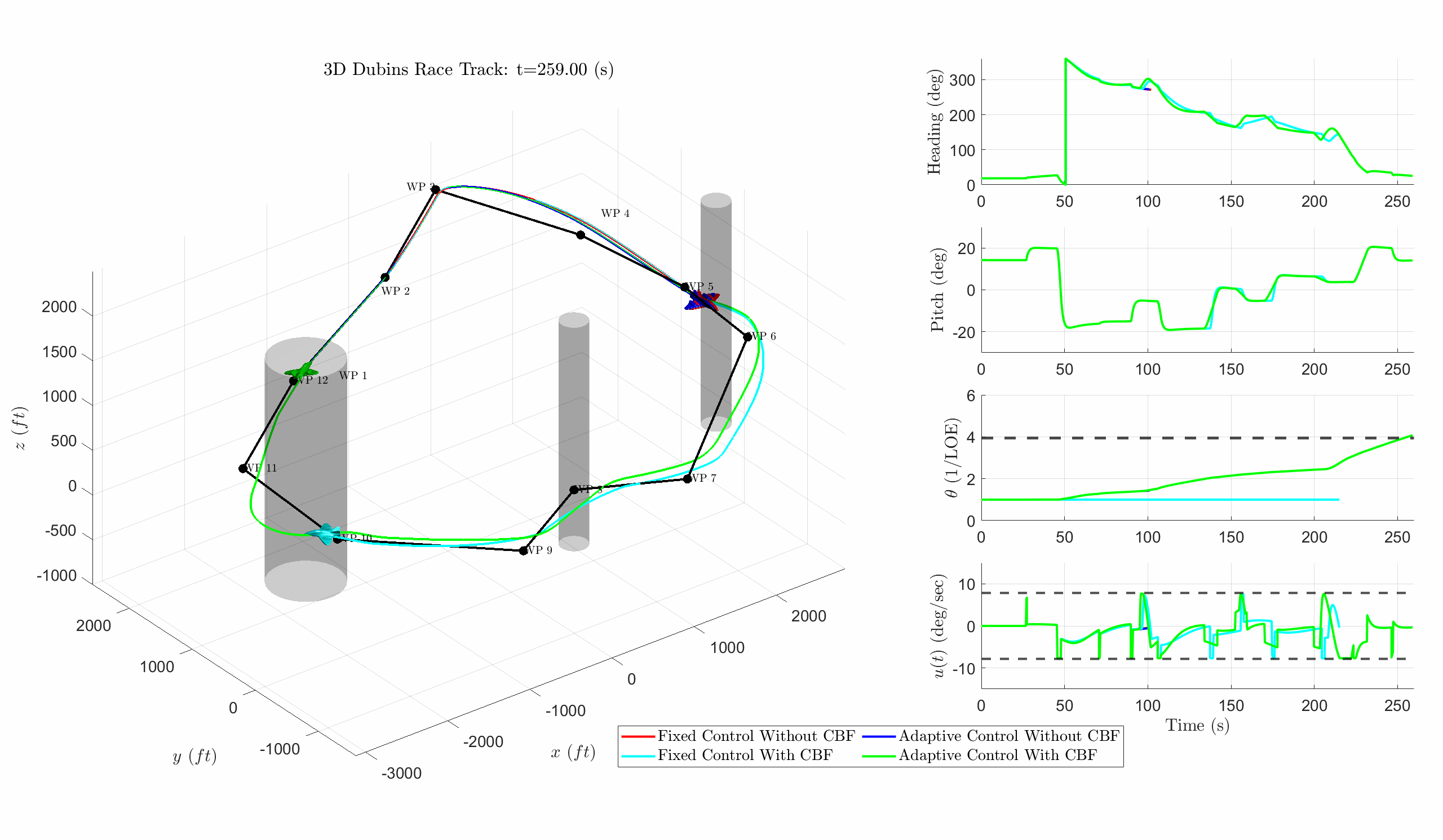
Figure 2: Shows a DV following a complex 3D waypoint path with changes in altitude and no-fly zones. In red is the PID controller and in blue is the adaptive controller (AC). Cyan depicts PID with CBF and green depicts AC with CBF. The adaptive design continues to succeed despite LOE. When state constraints and a LOE are present, AC + Control Barrier Functions (CBF) are required to guarantee. In the animation when the plane stops, that means the vehicle has entered a no fly zone (violated a state constraint).
Conclusion
Dubins Vehicle (DV) represents a canonical model for path-following and waypoint guidance problems. This work proposes an integrative Adaptive Control plus Control Barrier Function (AC+CBF) architecture that ensures the DV follows prescribed paths under both loss of control effectiveness and state plus input constraints. By combining online LOE estimation, Lyapunov-based adaptation, and CBF safety guarantees, the approach achieves resilient, constraint-satisfying navigation.